Quick Sort:
Quick sort is a divide
and conquer algorithm. In merge sort, an array a[1:n] is divided at its
mid-point into sub arrays which are independently sorted and later merged. But
in quick sort, the division of an array into two sub arrays is made so that the
sorted sub arrays do not need to be merged later. This is accomplished by
re-arranging the elements in a[i:n] such that a[i]≤a[j] for all I between 1 to
m and all j between m+1 to n, for some 1≤m≤n. Thus the elements in a[1:m] and
a[m+1:n] can be independently sorted. No merge is needed.
The re-arrangement of the elements is accomplished by picking some
element of a[], say t=a[s] and then re-ordering the other elements so that all
the elements appearing before t in a[1:n] ≤t and all the elements appearing
after t are greater than t. This re-arrangement is referred to as partitioning.
§ Algorithm:
Algorithm qs(a,b,e)
{
if (e>b)
{
l=partition(a,b,e);
qs(a,b,l-1);
qs(a,l+1,e);
}
}
Algorithm
Partition(a,b,e)
{
pivot=a[b];
start=b;
end=e;
while(start<end)
{
while(a[start]<=pivot
and start<end)
{
start=start+1;
}
while(a[end]>pivot)
{
end=end-1;
}
if(start<end)
{
swap(a[start],
a[end]);
}
}
a[b]=a[end];
a[end]=pivot;
return end;
}
§ Analysis:
Time taken by quick sort for an array of
n element is:
where k is the number of element smaller
than the pivot.
Worst Case:
The worst case occurs when the partition
process always picks the greatest or smallest element as pivot. If we consider
our partition strategy showed above where first is always picked as pivot, then
the worst case would occur when the array is already sorted in increasing or
decreasing order. Thus the recurrence relation becomes:
Here, the time complexity is O(n2).
Best case:
The Best case occurs when the partition process always picks the middle element as pivot. Thus the recurrence relation becomes: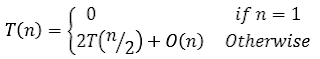
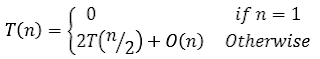
Here, the time complexity
is O(nlogn).
No comments:
Post a Comment